薛定谔的最优颜料
没错,就是那位薛定谔。
早在 1920 年,薛定谔就发表了一篇名为 Theorie der Pigmente von größter Leuchtkraft 的文章,原文是德语,但好在我们有精通多国语言的 LLM 帮忙。这篇文章大致探讨了各种颜料的反射特性,为什么颜料所能达到的颜色饱和度不如纯光谱光,并推导了一种理论上的“最优颜料”,这种颜料的反射率在波长上是二值的,要么完全反射,要么完全不反射。
这时候,CIE 尚未推出 CIE 1931 XYZ 颜色匹配函数,也早于 1924 年的 $V(\lambda)$,文中“亮度”(Helligkeit)的定义有关一种“量”(Quantität),是三种颜色的量的综合,也算是之后颜色匹配函数和亮度的雏形。在亮度等基础概念尚且模糊的时候,有关最优颜色的讨论就已经开始了,是色彩科学中,历史最丰富的话题之一。
MacAdam 最优色
1935 年,已经对亮度和颜色有了量化的标准,MacAdam 发表文章,提出了最优色的概念,原文为“具有最大视觉效率的颜色材料”。
MacAdam 最优色是“理论物体色立体”(Object Colour Solid)在亮度维度上的外表面,即在特定光源下,所有仅靠反射(无荧光、不自发光)的物体理论上所能呈现颜色集合的亮度上限。该立体由所有物理上可能的反射光谱在颜色空间中所张成,包含了所有的真实物体色,而其表面则代表理论上的极限。
MacAdam 最优色(Optimal Colour)特指该立体中,在每一组色度坐标(x, y 或 u’, v’ 等)上所能达到的最大亮度值所对应的颜色,即“在给定色度下,亮度最高的理论物体色”。比如,这是某光源下的 MacAdam 最优色的亮度伪色图。
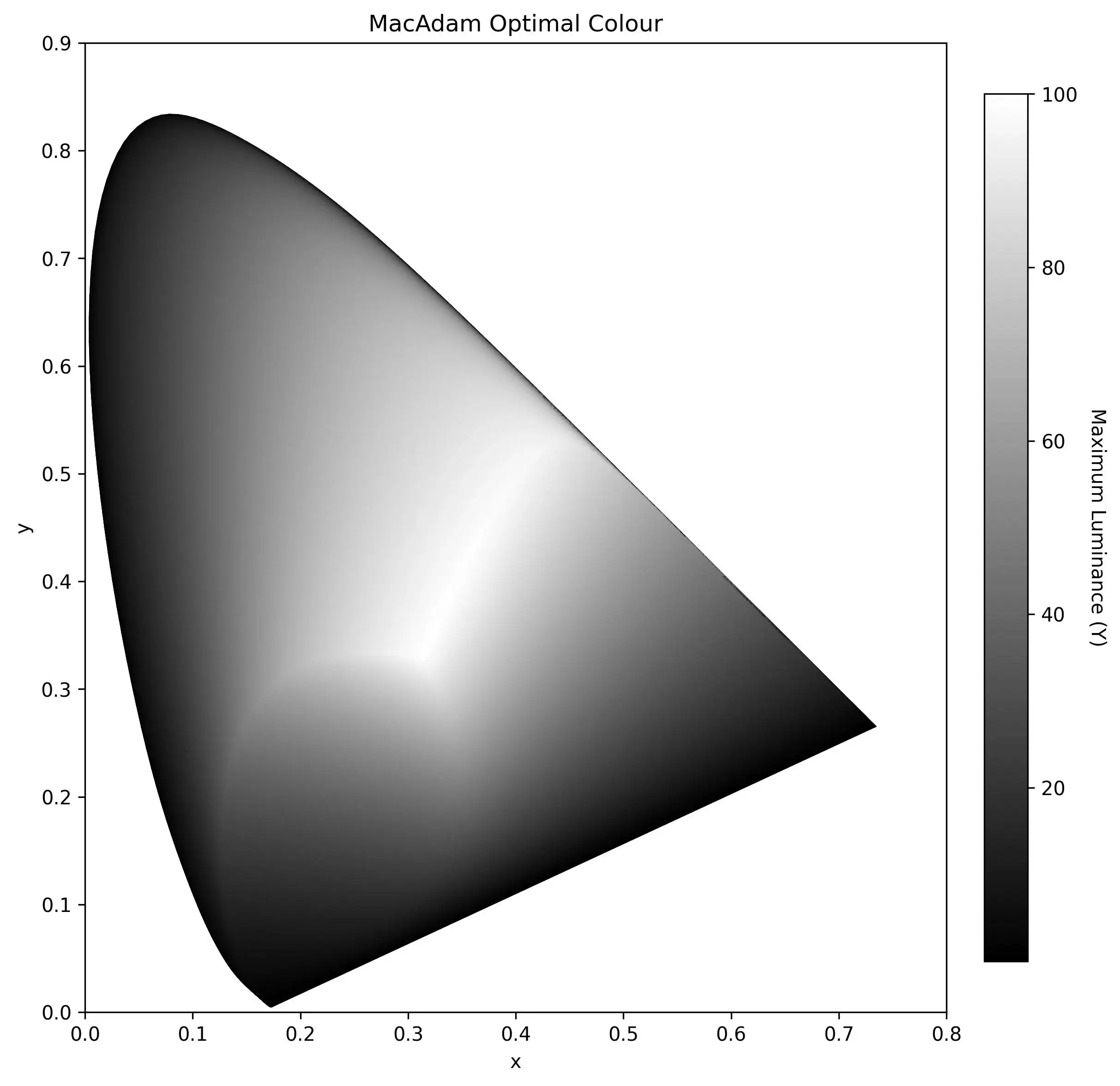
实现这些最优色所需的反射率函数呈“二值方波”形式,且仅含两个跃变点。虽然这类反射率在现实中不可能实现,但它们构成了物体色的理论天花板。
方波反射率的证明
薛定谔和 MacAdam 都证明了,要实现最优色,其反射率必须是一个二值的方波,且跃变点不超过两个,它们的证明方法基于物理分析和直觉。
下面,我们通过变分法和拉格朗日乘子法,从数学上证明,对于任意给定的色坐标,达到最大亮度时,对应的反射率是一个“方波”。
我们先用数学语言表示这些条件和问题:
题干
- 反射率 R,是一个关于波长 $\lambda$ 的函数,取值在 0-1 之间。
- 颜色匹配函数 CMF,用于将光谱功率分布转换为三刺激值 XYZ,也是关于波长的函数,记为 $\bar{x}$,$\bar{y}$,$\bar{z}$。
- 光源的光谱功率分布 I 和反射后的光谱功率分布 P。
- 任意给定的色品坐标 $x_0$,$y_0$。
求证:对于给定的色品坐标 $(x_{0}, y_{0})$,存在一个反射率函数 $R(\lambda)$,使得 $Y$ 取得最大值。此时,$R(\lambda)$ 的取值仅有 0 和 1 两种可能。
具体证明
我们可以通过变分法和拉格朗日乘子法证明,对于任意给定的色坐标,能够达到最大亮度的反射光谱必然是一个“方波”函数,其取值仅为 0 或 1。
为了使推导更清晰,我们分两步进行:首先,在一个理想化的等能谱光源下证明结论;然后,将此结论推广到任意光源,证明光源的光谱分布不影响最优反射率的“方波”形式。
第一步:在等能谱光源下的证明
我们先假设光源为等能谱光源,即其光谱功率分布 $I(\lambda)$ 是一个常数。为简化计算,可设 $I(\lambda)=1$ 和 $k=1$。此时,三刺激值为:
$$ X = \int R(\lambda) \bar{x}(\lambda) \, d\lambda, \quad Y = \int R(\lambda) \bar{y}(\lambda) \, d\lambda, \quad Z = \int R(\lambda) \bar{z}(\lambda) \, d\lambda $$我们的目标是在满足色品坐标 $(x_0, y_0)$ 约束的条件下,最大化亮度 $Y$。 目标函数为:
$$ \text{Maximize} \quad Y = \int R(\lambda) \bar{y}(\lambda) \, d\lambda $$色品约束 $x=x_0$ 和 $y=y_0$ 可变换为两个等价的线性约束。为书写简洁,我们定义 $z_0 = 1 - x_0 - y_0$。约束条件为:
$$ \int R(\lambda) \left( \bar{x}(\lambda) - \frac{x_0}{y_0} \bar{y}(\lambda) \right) d\lambda = 0 $$$$ \int R(\lambda) \left( \bar{z}(\lambda) - \frac{z_0}{y_0} \bar{y}(\lambda) \right) d\lambda = 0 $$这是一个约束优化问题。我们引入拉格朗日乘子 $\mu_1, \mu_2$,构造辅助泛函 $J[R]$。通过将目标函数和约束条件组合,问题转化为最大化 $J[R]$:
$$ J[R] = \int R(\lambda) f(\lambda) \, d\lambda $$其中,被积函数的核心部分 $f(\lambda)$ 由下式给出:
$$ f(\lambda) = \bar{y}(\lambda) - \mu_1 \left( \bar{x}(\lambda) - \frac{x_0}{y_0} \bar{y}(\lambda) \right) - \mu_2 \left( \bar{z}(\lambda) - \frac{z_0}{y_0} \bar{y}(\lambda) \right) $$将上式按颜色匹配函数 (CMF) 整理,可得:
$$ f(\lambda) = c_1 \bar{x}(\lambda) + c_2 \bar{y}(\lambda) + c_3 \bar{z}(\lambda) $$这里的 $c_1, c_2, c_3$ 是仅依赖于 $(x_0, y_0)$ 和乘子 $(\mu_1, \mu_2)$ 的常数。这表明 $f(\lambda)$ 始终是 CMF 的一个线性组合。
要在物理约束 $0 \le R(\lambda) \le 1$ 下最大化积分 $J[R]$,我们在每个波长 $\lambda$ 上都应独立地使被积项 $R(\lambda) f(\lambda)$ 最大:
- 若 $f(\lambda) > 0$,应取 $R(\lambda) = 1$。
- 若 $f(\lambda) < 0$,应取 $R(\lambda) = 0$。
- 若 $f(\lambda) = 0$,则 $R(\lambda)$ 的取值不影响结果,这些点构成了从 0 到 1 的切换点。
因此,最优反射率 $R(\lambda)$ 的取值只可能是 0 或 1,其函数图像呈“方波”状,切换点是该 CMF 线性组合的零点。
第二步:推广至任意光源
现在考虑任意光源 $I(\lambda)$,其中 $I(\lambda) > 0$。三刺激值公式变为:
$$ X = k \int R(\lambda) I(\lambda) \bar{x}(\lambda) \, d\lambda $$以及类似形式的 $Y$ 和 $Z$。
重复上述推导,目标函数和约束条件中的每个积分项都会被乘上 $I(\lambda)$。最终的辅助泛函变为:
$$ J[R] = \int R(\lambda) I(\lambda) f(\lambda) \, d\lambda $$其中 $f(\lambda)$ 的定义与第一步完全相同,它依然是 CMF 的线性组合,其形式不依赖于光源。
为了最大化 $J[R]$,我们需要在每个波长上最大化 $R(\lambda) I(\lambda) f(\lambda)$。由于光源谱分布 $I(\lambda)$ 恒为正,该项的符号完全由 $f(\lambda)$ 的符号决定。因此,选择 $R(\lambda)$ 的策略与第一步完全一致。
这证明了对任意光源,特定色度下的最优色,其对应的反射率谱必然是一个取值仅为 0 和 1 的方波函数。其“形状”(即 0/1 切换点的位置)仅由 CMF 的线性组合决定,与光源无关。
MacAdam 最优色的计算方法
一种直接的思路是:根据输入的色坐标 xy,反解出对应的拉格朗日乘子 $\mu_1\mu_2$,然后找到 CMF 线性组合后的零点波长,依此构建方波反射率并计算对应的亮度。但从 xy 求拉格朗日乘子是一个非线性过程,没有显式的解法,但可以从另外的角度入手,快速的求解最优色亮度。
关键在于,CMF 的线性组合多数情况下最多只能产生两个零点(端点除外),使得方波反射率要么是带通,要么是带阻。
利用这个特性,我们可以很快速的遍历所有的反射率,建立一个二维的查找表,输入色坐标,查找对应的最大亮度值。
具体操作是,设定两个切换点波长 $\lambda_1 \lambda_2$,一个从短波向长波移动,一个从长波向短波移动,每次都计算这两个切换点波长形成的带通反射率和带阻反射率对应的色坐标和亮度。形成一个 $Y=f(x,y)$ 的查找表。
意义
MacAdam 最优色是衡量打印机等设备颜色表达能力的一个理论基准。任何反射式设备的色域都不可能超越 MacAdam 极限所定义的范围,这为色彩管理和广色域技术的发展提供了理论天花板。
而在 HDR 时代,MacAdam 最优色的概念似乎又能发挥不同以往的新用途和新启发。